CSP考前佛脚

1 set

1.1 set 的定义

set<int>s;
set<int>::iterator it;//定义迭代器

1.2 set 的各种函数

s.begin(); // 返回第一个元素的迭代器
cout<<*s.begin(); // 输出最小值

s.end(); // 返回最后一个元素的下一个的迭代器
set<int>::iterator it=s.end();
it--;
cout<<*it; // 输出最大值
cout<<*(s.end()-1); // 非法操作：set的迭代器不是一个数值，不能做减法。
// 因为set不支持下标访问，它是一棵树（堆）。
// 而it--是支持的。

//与vector和数组的排序比较
vector <int> a;
sort(a.begin(),a.end()); // end()不用加一
const int maxn=1e5;
int arr[maxn];
sort(arr,arr+maxn+1); // 需要手动加一

s.rbegin(); // 倒着的最后一个迭代器
// 所以输出最大值不用 end() ，可以写成：
cout<<*s.rbegin();

s.erase(5); // 把 s 中的 5 删除（值）
s.erase(s.upper_bound(5)); // 删除第一个大于5的元素（迭代器）
s.erase(s.begin()); // 把 s 中的最小值删除（迭代器）
s.erase(*s.begin()); // 把 s 中的最小值删除（值，等价于上面一行）

set<int>::iterator it = s.find(3);
//如果有 3 就返回 3 的迭代器，否则返回 s.end() 。

s.count(3);
// 返回s中有几个3
// 注意：返回值只会是 0 或 1 ，因为 set 会自动去重！
// 所以 find 可以代替 count ，因为 find 还可以返回迭代器，比 count 更好！

// 其他函数
s.insert();
s.size();
s.clear();
s.lower_bound(); // 大于等于
s.upper_bound(); // 严格大于

set 可当作“双端去重优先队列”用，因为内部是从小到大排序的。

2 multiset

2.1 定义方式

真正的“双端优先队列”。

muiltiset<int>ms; // 可重集合

2.2 内建函数

ms.count(3); // 返回 3 的出现次数
ms.erase();
// erase() 函数，如果传入一个值，会删掉所有这个值的元素；
// 如果传入一个迭代器，那么只会删去这个迭代器的元素。

其它函数和 set 一样，不过多赘述。

3 map

3.1 基础知识

map<int,int>m;
m.insert({5,6}); // 等价于 m[5]=6;
m.insert({5,7}); // 等价于 m[5]=7;
cout<<m.count(5)<<endl; // 输出 1 ，因为已经被覆盖了
cout<<m.count(6)<<endl;
if(m[6]==0){
	cout<<"没有6"<<endl;
}
if(m.count(6)){
	cout<<"有6"<<endl;
}

想一想：上面的代码会输出 有6 还是 没有6 呢？

正确输出为：

1
0
没有6
有6

注意，在执行第6行引用了 m[6] ，此时 map 会自动为 m[6] 对应一个 0 ，所以在下面的代码中出现了 {6,0} 的键值对。

3.2 lower_bound()

// map 的 lower_bound() 方法
map<int,int>m;
m[10]=20;
m[12]=7;
m[7]=6;
map<int.int>::iterator it=m.lower_bound(8); // 找到第一个键值大于 8 的
cout<<it->fisrt<<" "<<it->second<<endl; // 与下面的等价
cout<<(*it).first<<" "<<(*it).second<<endl;
// 注意：不能使用 *it.first ，会报错，因为 * 的优先级比 . 低，而 first 没有 * 操作。

4 默认数据类型小讲堂

1
1ll
1ull
1<<10
1<<40ll // 爆掉，因为对 int 左移

cout<<10000000000<<endl;
// 输出 10000000000，而没有爆 int ，因为 c++ 会在你写下数字的时候自动选择数据类型

cout<<1000000*1000000<<endl;
// 会爆掉

cout<<1000000ll*1000000<<endl;
// 不会爆掉

5 比较大样例输出正确性

5.1 使用 Hash

certutil -hashfile <filepath>

这能得到两个文件的哈希值。

注意行末的换行，如果你的程序输出文件比大样例多/少了一个换行，哈希值也会完全不一样。

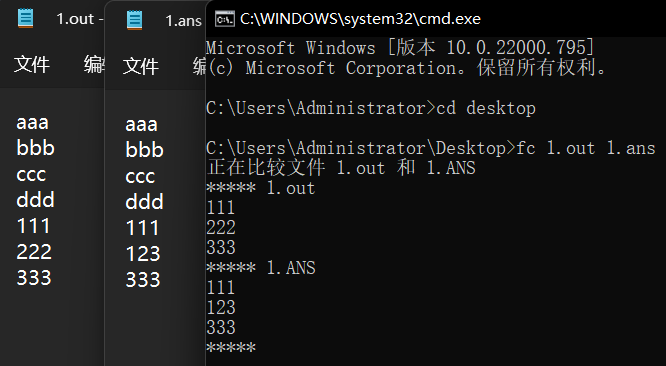
5.2 使用 fc 命令

fc <filepath1> <filepath2>

如图：

6 位运算

1. lowbit(x) = x & -x;
2. 全排列 x 的二进制子集：

   for(int i=x;i;i=x&(i-1)){
    cout<<i<<endl;
   }
   

7 排序

7.1 常见的排序

1. 冒泡排序（ $n$ 趟，每趟从前往后，当前大就交换相邻）
2. 计数排序（排结构体时，用邻接表限制插入排序，稳定）
3. 选择排序（每次找到最大的，从很远的位置换过来，不稳定）
4. 插入排序（复杂度 $O(N^2)$ 无法优化；但省内存；反冒泡，稳定）

   // 插入排序示例
   for(int i=1;i<=n;i++){
    for(int j=i;j>=2;j--){
        if(a[j]>a[j-1]){
            swap(a[j],a[j-1]);
        }
    }
   }
   

5. 快速排序（分治，用了分治的思想，不能说用了递归的思想；时间复杂度不稳定，排序不稳定）
6. 归并排序（分治，稳定， $O(nlogn)$ ，时间复杂度也稳定）
7. 基数排序（优先级低到高，从个位、十位到百位……排序， $O(nlgn)$ ，基于计数排序，稳定）
8. 桶排序（分成一些范围的桶，如1~10，11~20……，然后对每个桶内再进行排序，👎）
9. 堆排序（不稳定）
10. 希尔排序（不稳定，👎）

7.2 关于比较次数

1. 求最大/小值： $n-1$ 次。
2. 冒泡排序/选择排序： 第 $i$ （从 1 开始计数）趟比较 $n-i$ 次。
3. 通常代值 $1$, $2$ 。

8 存图 - 链式前向星

优点：常数更小

以下代码转自 https://blog.csdn.net/sugarbliss/article/details/86495945 ：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1005;//点数最大值
int n, m, cnt;//n个点，m条边
struct Edge
{
    int to, w, next;//终点，边权，同起点的下一条边的编号
}edge[maxn];//边集
int head[maxn];//head[i],表示以i为起点的第一条边在边集数组的位置（编号）
void init()//初始化
{
    for (int i = 0; i <= n; i++) head[i] = -1;
    cnt = 0;
}
void add_edge(int u, int v, int w)//加边，u起点，v终点，w边权
{
    edge[cnt].to = v; //终点
    edge[cnt].w = w; //权值
    edge[cnt].next = head[u];//以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[u] = cnt++;//更新以u为起点上一条边的编号
}
int main()
{
    cin >> n >> m;
    int u, v, w;
    init();//初始化
    for (int i = 1; i <= m; i++)//输入m条边
    {
        cin >> u >> v >> w;
        add_edge(u, v, w);//加边
        /*
        加双向边
        add_edge(u, v, w);
        add_edge(v, u, w);
        */
    }
    for (int i = 1; i <= n; i++)//n个起点
    {
        cout << i << endl;
        for (int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边
        {
            cout << i << " " << edge[j].to << " " << edge[j].w << endl;
        }
        cout << endl;
    }
    return 0;
}
/*
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
*/

9 概率与期望

打靶问题： $n$ 个靶子，每个靶子给一个命中概率 $a[i]$ （表示 $a[i]$ 分之一，问期望多少次能够连续命中 $n$ 个靶子。

for(int i=1;i<=n;i++){
	ans[i]=(ans[i-1]+1)*a[i];
	// 走到第 i 个靶需要付出代价
}

打靶问题2： $n$ 个靶子，每个靶子给一个命中概率 $\frac{a[i]}{b[i]}$ ，问期望多少次能够连续命中 $n$ 个靶子。

for(int i=1;i<=n;i++){
	ans[i]=(ans[i-1]+1)*b[i]*inv[a[i]];
	// 走到第 i 个靶需要付出代价
}