文章

CSP 考前膜拜模版

发表于
Preview Image
作者 Dignite
・ ・ 15 分钟阅读

0. 重要提示

0.1 重定向输入输出

1
2
3
4
5
6

int main(){
	freopen("decode.in","r",stdin);
	freopen("decode.out","w",stdout);
    // ...
    return 0;
}

0.2 文件目录

截屏2023-10-21 08.58.11.png

截屏2023-10-21 08.58.46.png

0.3 试题

CSP-J 2023

1. P3865 ST 表

题目描述

给定一个长度为 $N$ 的数列，和 $ M $ 次询问，求出每一次询问的区间内数字的最大值。

输入格式

第一行包含两个整数 $N,M$，分别表示数列的长度和询问的个数。

第二行包含 $N$ 个整数（记为 $a_i$），依次表示数列的第 $i$ 项。

接下来 $M$ 行，每行包含两个整数 $l_i,r_i$，表示查询的区间为 $[l_i,r_i]$。

输出格式

输出包含 $M$ 行，每行一个整数，依次表示每一次询问的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10

8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8

样例输出 #1

1
2
3
4
5
6
7
8

9
9
7
7
9
8
7
9

提示

对于 $30\%$ 的数据，满足 $1\le N,M\le 10$。

对于 $70\%$ 的数据，满足 $1\le N,M\le {10}^5$。

对于 $100\%$ 的数据，满足 $1\le N\le {10}^5$，$1\le M\le 2\times{10}^6$，$a_i\in[0,{10}^9]$，$1\le l_i\le r_i\le N$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <bits/stdc++.h>
using namespace std;
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}
const int maxn=1e6+5;
int n,m;
int a[maxn];
int st[maxn][(int)log2(maxn)+1];
int l,r;
int solve(int l,int r){
    return max(st[l][(int)log2(r-l+1)],st[r-(1<<int(log2(r-l+1)))+1][(int)log2(r-l+1)]);
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++){
        a[i]=read();
        st[i][0]=a[i];
    }
    for(int j=1;j<=log2(n);j++){
        for(int i=1;i+(1<<(j-1))<=n;i++){
            st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
        }
    }
    while(m--){
        l=read(),r=read();
        cout<<solve(l,r)<<"\n";
    }
    return 0;
}

2. P4779 【模板】单源最短路径（标准版）

题目背景

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

$100 \rightarrow 60$；

$\text{Ag} \rightarrow \text{Cu}$；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

题目描述

给定一个 $n$ 个点，$m$ 条有向边的带非负权图，请你计算从 $s$ 出发，到每个点的距离。

数据保证你能从 $s$ 出发到任意点。

输入格式

第一行为三个正整数 $n, m, s$。 第二行起 $m$ 行，每行三个非负整数 $u_i, v_i, w_i$，表示从 $u_i$ 到 $v_i$ 有一条权值为 $w_i$ 的有向边。

输出格式

输出一行 $n$ 个空格分隔的非负整数，表示 $s$ 到每个点的距离。

样例 #1

样例输入 #1

1
2
3
4
5
6
7

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

1

0 2 4 3

提示

样例解释请参考 数据随机的模板题。

$1 \leq n \leq 10^5$；

$1 \leq m \leq 2\times 10^5$；

$s = 1$；

$1 \leq u_i, v_i\leq n$；

$0 \leq w_i \leq 10 ^ 9$,

$0 \leq \sum w_i \leq 10 ^ 9$。

本题数据可能会持续更新，但不会重测，望周知。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

#include <bits/stdc++.h>
using namespace std;
int n,m,s;
struct node{
    int a,val;
    bool operator < (node b) const{
        return val>b.val;
    }
};
vector <node> G[100010];
priority_queue <node> q;
int dis[100010];
int main(){
    cin>>n>>m>>s;
    int a,b,c;
    for(int i=1;i<=m;i++){
        cin>>a>>b>>c;
        G[a].push_back({b,c});
    }
    q.push({s,0});
    memset(dis,0x3f,sizeof dis);
    dis[s]=0;
    while(!q.empty()){
        node now=q.top();
        q.pop();
        if(now.val!=dis[now.a])continue;
        for(int i=0;i<G[now.a].size();i++){
            node nxt=G[now.a][i];
            if(dis[nxt.a]>dis[now.a]+nxt.val){
                q.push({nxt.a,dis[now.a]+nxt.val});
                dis[nxt.a]=now.val+nxt.val;
            }
        }
    }
    for(int i=1;i<=n;i++){
        cout<<dis[i]<<" ";
    }
    return 0;
}

3. P3366【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 $N,M$，表示该图共有 $N$ 个结点和 $M$ 条无向边。

接下来 $M$ 行每行包含三个整数 $X_i,Y_i,Z_i$，表示有一条长度为 $Z_i$ 的无向边连接结点 $X_i,Y_i$。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

样例 #1

样例输入 #1

1
2
3
4
5
6

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

样例输出 #1

1

7

提示

数据规模：

对于 $20\%$ 的数据，$N\le 5$，$M\le 20$。

对于 $40\%$ 的数据，$N\le 50$，$M\le 2500$。

对于 $70\%$ 的数据，$N\le 500$，$M\le 10^4$。

对于 $100\%$ 的数据：$1\le N\le 5000$，$1\le M\le 2\times 10^5$，$1\le Z_i \le 10^4$。

样例解释：

所以最小生成树的总边权为 $2+2+3=7$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#include <bits/stdc++.h>
using namespace std;
int n,m;
int x,y,z;
const int maxn=5010;
struct ed{
    int val,x,y;
};
vector <ed> edges;
bool cmp(ed x,ed y){
    return x.val<y.val;
}
int numberOfEdges=0;
int fa[maxn];
int find(int x){
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y){
    int fax=find(x),fay=find(y);
    if(fax!=fay){
        fa[fax]=fay;
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        fa[i]=i;
    }
    for(int i=1;i<=m;i++){
        cin>>x>>y>>z;
        if(x==y)continue;
        edges.push_back({z,x,y});
    }
    int ans=0;
    sort(edges.begin(),edges.end(),cmp);
    for(auto i:edges){
        int fax=find(i.x),fay=find(i.y);
        if(fax!=fay){
            numberOfEdges++;
            merge(i.x,i.y);
            ans+=i.val;
        }
    }
    if(numberOfEdges!=n-1){
        cout<<"orz"<<endl;
        return 0;
    }
    cout<<ans;
    return 0;
}

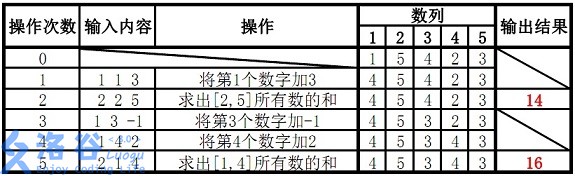
4. 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  • 将某一个数加上 $x$

  • 求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

  • 1 x k 含义：将第 $x$ 个数加上 $k$

  • 2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

1
2

14
16

提示

【数据范围】

对于 $30\%$ 的数据，$1 \le n \le 8$，$1\le m \le 10$；
对于 $70\%$ 的数据，$1\le n,m \le 10^4$；
对于 $100\%$ 的数据，$1\le n,m \le 5\times 10^5$。

数据保证对于任意时刻，$a$ 的任意子区间（包括长度为 $1$ 和 $n$ 的子区间）和均在 $[-2^{31}, 2^{31})$ 范围内。

样例说明：

故输出结果14、16

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

#include<cstdio>
#include<iostream>
using namespace std;
const int maxn=5e5+10;
int n,m;
int a[maxn];
int bit[maxn];
int k,x,y;
int lowbit(int x){
    return x & -x;
}
void change(int x,int y){
    while(x<=n){
        bit[x]+=y;
        x+=lowbit(x);
    }
}
int query(int x){
    int ans=0;
    while(x>0){//边界条件x>0!
        ans+=bit[x];
        x-=lowbit(x);
    }
    return ans;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        change(i,a[i]);//一开始都是0，要初始化加上a[i]
    }
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&k,&x,&y);
        if(k==1){
            change(x,y);//将第x个数加上y
        }else{
            printf("%d\n",query(y)-query(x-1));//求出区间和
        }
    }
    return 0;
}

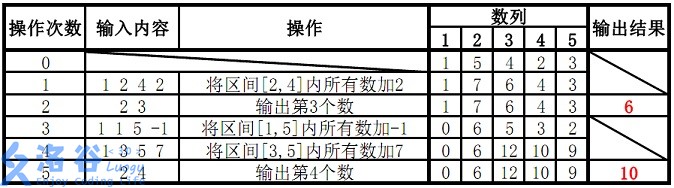
5. 【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  1. 将某区间每一个数加上 $x$；

  2. 求出某一个数的值。

输入格式

第一行包含两个整数 $N$、$M$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $N$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i $ 项的初始值。

接下来 $M$ 行每行包含 $2$ 或 $4$个整数，表示一个操作，具体如下：

操作 $1$： 格式：1 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$；

操作 $2$： 格式：2 x 含义：输出第 $x$ 个数的值。

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

样例输出 #1

1
2

6
10

提示

样例 1 解释：

故输出结果为 6、10。

数据规模与约定

对于 $30\%$ 的数据：$N\le8$，$M\le10$；

对于 $70\%$ 的数据：$N\le 10000$，$M\le10000$；

对于 $100\%$ 的数据：$1 \leq N, M\le 500000$，$1 \leq x, y \leq n$，保证任意时刻序列中任意元素的绝对值都不大于 $2^{30}$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include <bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
int a[maxn];
int bit[maxn];
int n,m;
int cmd,x,y,k;
// 差分思想，用bit[x]表示第i个数
int lowbit(int x){
    return x&-x;
}
void add(int x,int y){
    while(x<=n){
        bit[x]+=y;
        x+=lowbit(x);
    }
}
int query(int x){
    int ans=0;
    while(x>0){//边界条件x>0!
        ans+=bit[x];
        x-=lowbit(x);
    }
    return ans;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        add(i,a[i]);
        add(i+1,-a[i]);
    }
    for(int i=1;i<=m;i++){
        cin>>cmd;
        if(cmd==1){
            cin>>x>>y>>k;
            add(x,k);
            add(y+1,-k);
        }else{
            cin>>x;
            cout<<query(x)<<endl;
        }
    }
    return 0;
}

6. 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  1. 将某区间每一个数加上 $k$。
  2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n, m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

  1. 1 x y k：将区间 $[x, y]$ 内每个数加上 $k$。
  2. 2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1

1
2
3
4
5
6
7

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

样例输出 #1

1
2
3

11
8
20

提示

对于 $30\%$ 的数据：$n \le 8$，$m \le 10$。
对于 $70\%$ 的数据：$n \le {10}^3$，$m \le {10}^4$。
对于 $100\%$ 的数据：$1 \le n, m \le {10}^5$。

保证任意时刻数列中所有元素的绝对值之和 $\le {10}^{18}$。

【样例解释】

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=8e5+10;
int tree[maxn];
int lazy[maxn];
int n,m;
void push_up(int p){
    tree[p]=tree[p*2]+tree[p*2+1];
}
void push_down(int p,int l,int r){
    lazy[p*2]+=lazy[p];
    lazy[p*2+1]+=lazy[p];
    int mid=(r+l)/2;
    tree[p*2]+=lazy[p]*(mid-l+1);
    tree[p*2+1]+=lazy[p]*(r-mid);
    lazy[p]=0;
}
void build(int s,int t,int p){
    if(s==t){
        cin>>tree[p];
        return;
    }
    int mid=(s+t)/2;
    build(s,mid,p*2);
    build(mid+1,t,p*2+1);
    push_up(p);
}
void update(int l,int r,int s,int t,int p,int v){
    if(l<=s&&t<=r){
        lazy[p]+=v;
        tree[p]+=v*(t-s+1);
        return;
    }
    push_down(p,s,t);
    int mid=(s+t)/2;
    if(mid>=l)
        update(l,r,s,mid,p*2,v);
    if(mid<r)
        update(l,r,mid+1,t,p*2+1,v);
    push_up(p);
}
int query(int l,int r,int s,int t,int p){
    if(l<=s&&t<=r){
        return tree[p];
    }
    int mid=(s+t)/2;
    int ans=0;
    push_down(p,s,t);
    if(mid>=l){
        ans+=query(l,r,s,mid,p*2);
    }
    if(mid<r){
        ans+=query(l,r,mid+1,t,p*2+1);
    }
    return ans;
}
signed main(){
    cin>>n>>m;
    build(1,n,1);
    while(m--){
        int op,x,y,z;
        cin>>op;
        if(op==1){
            cin>>x>>y>>z;
            update(x,y,1,n,1,z);
        }else{
            cin>>x>>y;
            cout<<query(x,y,1,n,1)<<endl;
        }
    }
    return 0;
}
笔记本, OI
CSP
本文由作者按照 CC BY 4.0 进行授权

© Dignite. 保留部分权利。 由  提供CDN加速。

浙ICP备2023032699号 | 使用 Jekyll 主题 Chirpy