结构化学基础壹

发表于 2023/07/12

作者 Dignite

・・ 17 分钟阅读

约定：本文用加粗标记定义或概念，实验名称由斜体标注。本文中所有图片均为网图，侵删。

1. 经典核原子模型

1.1 电子的发现

如图，在一个两端各嵌有一个金属电极的玻璃管中施加几千伏特的高压，并将管中气体抽成真空。可以看到荧光屏上出现了一条笔直的荧光带。

给管中是假一个磁场（用磁铁吸引），可以观察到阴极射线发生了弯曲。该电子流具有负电荷。

利用该装置还能测出电子的电荷 $e$ 与其质量 $m$ 之比值，称作荷质比。

1.1.1 测定电子的速度

若电子的电荷为 $e$ 、速度为 $v$ ，电场强度为 $E$ ，磁场强度为 $H$ ，如果电子所受的磁力和电力相等，则有：

H \cdot e \cdot v = E \cdot e

即：

H \cdot v = E ⟺ v = \frac{E}{H}

这样就能算得电子的速度。

1.1.2 测定电子的电荷

$1909$ 年字母哥 $M i l l i k a n$ 设计的油滴实验可以巧妙地测出电子的电荷。在电场中喷入微小的油滴，并同入 X 光使空气电离，这样小油滴就能在电场力和重力之间平衡。所受电场力和电荷 $e$ 有关，而重力有和 $m$ 有关。 $m$ 是已知的量，若每个油滴只带有一个电荷，那么最小的电荷量 $e$ 就能求出。最终实验得到 $e = 1.6 \times 10^{- 19} C$ ，电子质量 $m_{e} = 9.11 \times 10^{- 31} k g$ 。

1.2 原子模型的发展史

1.2.1 早期的模型

$1897$ 年前后， $J . J . T h o m s o n$ 通过实验提出了葡萄干布丁模型。

$1911$ 年，英国物理学家 $R u t h e r f o r d$ 通过 $α$ 粒子散射实验，否定了汤姆森的模型，建立了核原子模型。

在该实验中，大部分粒子通过了金箔，并没有改变运动方向，少部分粒子发生偏转，更少部分被反弹或原路返回。该实验能够得出以下结论：

原子核内部很空旷，中间的有一个原子核且带正电。
整个原子的全部质量几乎都集中在这个原子核上。
带负电的电子高速在核外绕核转动。

估算金箔原子核的大小： $\frac{1}{2} m v^{2} = K \frac{Z_{1} e Z_{2} e}{r_{0}}$ ，其中左边为假定粒子的动能，右边为该粒子最靠近原子时转化成的库伦排斥势能。 $Z$ 分别表示两者的核电荷数（ $2$ 与 $79$ ）， $r_{0}$ 表示该最近的距离。

1.2.2 普朗克量子论

1.2.2.1 黑体辐射实验

绝对黑体是指能全部吸收辐射电磁波的物体（看上去就是完全黑色的，理想化模型），在受热时能发出连续波长的电磁辐射。下图为黑体在不同温度下，电磁辐射波长与强度的关系图像。

由图，虚线表示经典力学中，随着波长减小，辐射强度应该无限增大。然而在实验观测中，当波长进入了紫外区，出现了经典力学无法解释的现象。这就是紫外灾难。

$1900$ 年，普朗克第一次提出量子的概念。他认为，能量是不连续的，最小的能量单位称作量子。具体来说，一个量子的能量与其电磁波的频率成正比：

E = h v

其中， $h \approx 6.62607015 \times 10^{- 34} J \cdot s$ 称作普朗克常数， $v$ 为电磁波的频率。

例题：电磁辐射波长为 $122 m m$ 的光子能量为多少？

1.2.2.2 光电效应

爱因斯坦使用普朗克量子论解释了该实验，认为光由光子组成，它的能量也是不连续的。用公式来表示，就是：

h v = E = W + E_{k}

其中， $h v = E$ 即为光子碰撞到电子上，让电子吸收的能量。 $W$ 为电子克服原子对它的束缚进而逃逸的最小能量， $E_{k}$ 就是剩下的能量，全部转换为动能，用于电子获取速度。

由此可见，只有当 $E > W$ 时，提供的能量大于所需的最小能量，才能触发光电效应。而 $E$ 只和光子频率 $v$ 有关。这就必须使用量子的角度解释。

波长、波速与频率之间的关系： $λ = \frac{V}{v}$ ，即 $波长 = \frac{波速}{频率}$ 。当我们在研究标准的光的时候，可以将光速 $c$ 带入波速 $V$ 。

1.2.3 波尔 $B o h r$ 理论

要点：电子在轨道上，而轨道具有一定的能量。

1.2.3.1 $B a l m e r$ 经验公式

氢原子光谱上各个光的波长可由以下经验公式得出。其中 $n$ 为大于等于 $3$ 的正整数，通过变换 $n$ 的数值，可以得到多个 $λ$ ，这些波长都为氢原子所具有。

λ = \frac{3646.00 \times n^{2}}{n^{2} - 4}

进而可以计算波数：

\overset{―}{v} = \frac{1}{λ}

1.2.3.2 原子的轨道能量

E = - \frac{13.6 Z^{2}}{n^{2}} e V

其中， $Z$ 为核电荷数， $n$ 表示原子的第几层轨道。

当 $Z = 1, n = 1$ 时，氢原子 $K$ 层的半径为 $53 p m$ ，称作波尔半径。

离原子核越近，能量越低，越稳定。电子层（又称能层），从里到尾分别是 $K$ ， $L$ ， $M$ ， $N$ 。

1.3 微观粒子的波粒二象性

波粒二象性，指微粒既具有波动性又具有微粒性。并且这样的微观粒子不可能同时准确测定位置和动量，即测不准性或不确定性。

光的波性：干涉、衍射现象；
光的粒性：发射、吸收、光电效应。

1.3.1 爱因斯坦质能方程

当我们认为光子是粒子时，就可以认为它具有的能量为 $E = m c^{2}$ 。

然而，光又是波。故 $E = h v = m c^{2}$ 。

求得动量： $P = m c = \frac{h v}{c} = \frac{h}{λ}$ 。

电子的波长也就可以求得： $λ = \frac{h}{m V} = \frac{h}{P}$ 。

在等式 $h v = m c^{2}$ 中，我们可以看到，波动性和微粒性间搭建了一个桥梁。

1.3.2海森堡不确定原理

Δ x Δ P \geq \frac{h}{4 π} ⟺ Δ x \geq \frac{h}{4 π m Δ v} ⟺ Δ x Δ v \geq \frac{h}{4 π m}

在宏观世界中， $m$ 很大，所以 $Δ x Δ v$ 的误差很小。但在微观世界中， $m$ 很小，所以 $Δ x Δ v$ 的误差就难以预测了。

2. 薛定谔方程（简化版）

笔者只也只会介绍薛定谔方程中的几个参数，用以解释现代原子轨道理论。

2.1 前置技能

2.1.1 概率密度与电子云

在上一节的“海森堡不确定原理”中，我们已经知道了在微观世界中，粒子是难以预测的，所以之前波尔所提出的电子在轨道上运动，就显得有些问题了。电子的运动是不确定的、无法预测的，它不一定就在某个轨道上乖乖运动。那么，科学家们又该如何进一步研究呢？

实际上，我们并非非得要算出电子的运动轨迹。我们只要统计电子在各个位置的分布，就能大概了解电子的运动情况。

在一个空间中，我们定义概率密度 $ρ = \frac{P （概率）}{V （该处的体积）}$ 。

随后，我们将这个概率密度形象地表示在一个三维空间中，便得到了电子云（概率密度分布图）。

再将空间出现概率 $P = 90 %$ 的空间圈出来，就得到了电子云轮廓图。一个轮廓图对应一个原子轨道，一个原子当然有多个轨道。

2.1.2 波函数

$ψ$ 即为电子波函数，而 $ψ^{2}$ 就可代表电子在空间某点出现的概率密度。

2.1.3 径向分布图像

对于某个轨道， $ψ^{2}$ （某点的概率密度，纵轴）和与原子核中心的距离的关系图像，可由下图表示：

该图的物理意义是，单位厚度球壳内电子的分布概率。

2.2 方程的参数

2.2.1 主量子数 $n$

表示轨道离原子核的远近（决定了电子能级）。

可以取任意正整数，表示是第几层的轨道。

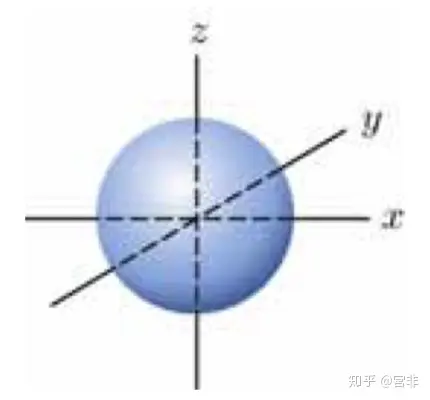
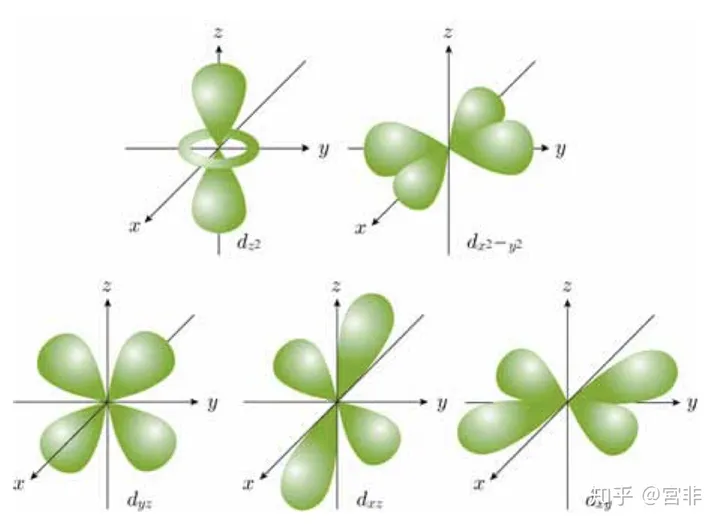
2.2.2 角量子数 $l$

决定了电子的轨道形状。

取值范围： $0, 1, 2, 3, 4, \dots, (n - 1)$ 。

分别对应： $s, p, d, f, g, \dots$ （例如对于第 $n = 2$ 层，可能为 $s$ 或 $p$ 轨道）。

不同的轨道有不同的形状。 $s$ 轨道为球形， $p$ 轨道为哑铃形， $d$ 轨道为花瓣形，等等。具体的形状图见下一小节。

2.2.3 磁量子数 $m$

决定了轨道的方向。

取值范围： $0, \pm 1, \pm 2, \dots, \pm m$ 。

注意：同一个 $n$ ，同时存在着不同的 $l$ 形轨道，而即便对于同一个 $l$ 形轨道，也同时存在着多个形状相同但方向不同的、也就是磁量子数 $m$ 不同的轨道。具体见下图。

2.2.2.1 $s$ 轨道的形状（只有一个）

2.2.2.2 $p$ 轨道的形状（共三个）

2.2.2.3 $d$ 轨道的形状（共五个）

例题： $n = 4, l = 2, m = 0$ 的轨道名称是什么？

2.2.4 自旋量子数 $m_{s}$

决定了这个电子在某个轨道上的“自转”方向。

取值只有两个： $+ \frac{1}{2}, - \frac{1}{2}$ 。分别表示正着转和反着转。

2.3 泡利不相容原理

不存在 $4$ 个量子数完全相同的电子。我们可以认为， $ψ$ 函数就是用来针对各个电子的。

2.4 小补充

2.4.1 能级的排布

每个轨道的能量由 $n$ 和 $l$ 确定。一般地， $n$ 越小， $l$ 越小，能量 $E$ 越小。

有时候，两个轨道的远近一样（ $n$ 一样），但能量不同（由 $l$ 不同引起），这就叫做能级分裂。

有时候，离核近的轨道反而能量更高，这就叫做能级交错，主要是因为受到了其他电子的排斥而能量增大。

如何准确地对各个能级进行排序呢？请见下节。

2.4.2 徐光宪近似规律

可以用来比较各个轨道能量的大小。

对于原子而言： $(n + 0.7 l)$ 越大，能级越大。
对于粒子而言： $(n + 0.4 l)$ 越大，能级越大。

2.4.3 能级的计算&屏蔽效应

对于单电子原子能级，有 $E = - \frac{13.6}{n^{2}} e V$ 。
对于多电子原子能级，有 $E = - \frac{Z^{* 2}}{n^{2}} e V = - \frac{(Z - σ)^{2}}{n^{2}} e V$ 。

其中， $Z$ 为核电荷数， $σ$ 为屏蔽常数。

为什么多电子原子能级要有减去 $σ$ 这样的操作呢？这就是由于屏蔽效应，内层电子会对外层电子产生排斥，相当于将原子核的引力削弱了一部分。

我们可以使用斯雷特规则来计算屏蔽常数 $σ$ 。

2.4.4 能级分裂的原因——钻穿效应

3 能级排布

3.1 能级排布规律图

由种种实验事实，人们总结出了一张图表，能帮助我们快速对能级进行排序。

由上图，我们可以看到，各个轨道的能量： $1 s < 2 s < 2 p < 3 s < 3 p < 4 s < 3 d < 4 p < 5 s$ ，等等。

3.2 电子排布式

我们将电子依次填入能量低到能量高的轨道。其中，每个 $s$ 轨道最多放 $2$ 个，每个 $p$ 轨道最多放 $6$ 个，每个 $d$ 轨道最多放 $10$ 个，每个 $f$ 轨道最多放 $14$ 个，等等。

接着，我们把放了多少个电子写到轨道的右上角。最后，我们还要将所有轨道按顺序排列。

以 $N a$ 为例： $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{1}$ 。

而 $K$ 可以简写： $[A r] 4 s^{1}$ 。

但 $19$ 种元素原子的外层电子分布有例外。其中主要为 $_{29} C u : [A r] 3 d^{10} 4 s^{1}$ 。

3.3 洪特规则

尽可能成单电子排列且自旋方向相同。
简并轨道、全空、半满或全满比较稳定。

笔记本, 化学

学习化学笔记结构化学

本文由作者按照 CC BY 4.0 进行授权